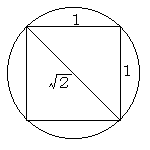暇つぶしに
数学（？）に挑戦しよう！

曲尺（かねじゃく）利用に潜む数学

皆さん，「曲尺」って知っていますか？ 　大工さんが使っている物差しです。右の図のような金属製の直角に曲がった定規で，表と裏に目盛りが刻まれています。別名を「差金（さしがね）」，「かねざし」，「かね」などとも言います。（注：図のように短いほうが右に向くようにした時見える目盛りが「表目」で，逆に短いほうが左に向くと「裏目（角目）」が見えます） 　曲尺を使って簡単に丸太の直径を知ることも，その直径から，その丸太からとれる正四角柱（角材）の１辺の長さを知ることができます。
そこには，皆さんが中学校の数学で学んだ知識が生かされていますので，簡単に紹介します。
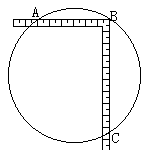
まず，右図のように，曲尺の直角の頂点Ｂを丸太の円周の１点に合わせます。 　直角を挟む２辺と丸太の円周との交点をＡ，Ｃとすると，線分ＡＣがこの丸太の直径となります。（直径の円周角は直角という円の性質）
線分ＡＣの長さを曲尺の裏目（裏の目盛り）で測れば，この丸太から切り出すことが出来る最大の角柱の１辺の長さが求められます。曲尺の裏目が，表目のルート２（約1.4.14）倍の目盛り幅となっているからです。（表の１目盛りが１ｃｍなら，裏の１目盛りはルート２ｃｍ，すなわち約１．４１４ｃｍ）だから，裏目で測った目盛は実際のルート２分の１となります。右下図参照
曲尺の裏目で直径を測れば，そのまま柱の一辺の長さが求められる仕組みになっています。（例えば直径が裏目で１０ｃｍなら，丸太の実際の直径は１．４倍の１４ｃｍ，その丸太からは１辺１０ｃｍの角柱を切り出すことができる）
右図のように，三平方の定理から正方形の「１辺の長さ」と「対角線の長さ」の比が求められ，丸太の直径と角柱の１辺の比が「ルート２：１」となることが解ります。 　よって，角柱の１辺の長さは，丸太の直径の「ルート２分の１」です。これを曲尺の裏目を使って求めるということです。

　

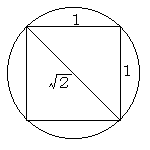　いかがでしたか，古来から伝わる大工さんたちの知恵，中学校で学んだ円や直角三角形などの図形の性質を利用しているんですね。曲尺は単なる長さを測ったり線を引くだけの道具でなく，計算機の役割もします。
　この他にも，曲尺を使って屋根などの勾配（傾き）を正確に測るのにも利用されています。
　

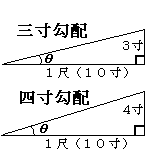
「三寸勾配」とか「四寸勾配」という言葉があります。三寸勾配とは，水平距離１尺（１０寸）に対して，垂直方向に３寸上がった勾配（傾き）を言います。四寸勾配とは水平距離１尺に対して，垂直方向に４寸上がった勾配です。すなわち，三寸勾配とは傾き「３／１０＝０．３」ということです。大工さんたちは曲尺を利用して様々な勾配を正確に造っていったのです。また，この値は三角比のｔａｎθの値ですね。
「寸（すん）と尺（しゃく）」 昔，日本で使われていた長さの単位で，１寸＝３，０３ｃｍ，１尺＝１０寸，１寸＝１０分です。寸の上には間（けん　１間＝６尺）もあり，面積の単位の坪(つぼ)（１坪は１間平方のことで，約３．３平方メートル）があります。このような単位を尺貫法(しゃかんほう)と言いますが，現在では法律で使用が禁じられています。元々の曲尺は尺や寸で目盛りが刻まれていました。

　曲尺はただ長さを測るだけでなく，測ることを応用して様々な活用法があるようです。表目と裏目の目盛りの違いは，計算尺（かけ算・わり算・平方根などを定規の目盛りを使って簡単に計算する道具で，電卓が普及して現在では使われなくなった）として利用するためなんですね。電卓や計算尺だったら，三角関数や幾何学の知識も必要ですし，一々紙にでもメモしなければ正確な寸法を出せないでしょう。曲尺を使いこなせば計算尺や電卓よりも便利な点も多いんです。このような使い方は奈良や平安時代からあったそうで，もし曲尺がなかったら，複雑な木組みで構成されているあの五重塔も造れなかったのではないかということです。
　肥後の石工たちも曲尺の表目と裏目の比がπ：１となっているものを利用したという話も残っています。曲尺は肥後の石橋を調べていく中で興味をいだいたものでした。この他にももっと興味深い活用法があるかとも思います。教えていただければ幸いです。（平成１１年１月3日）