解答; 2.5×3 を例に説明します。(三角形の相似を利用)
|
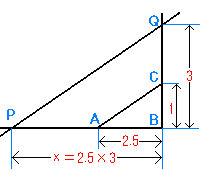 |
| 理由: PQとACが平行だから △PBQと△ABCは相似となり,対応する線分の比が等しいので PB:AB=QB:CB よって x:2.5=3:1 だから 外項の積と内項の積が等しいから x=2.5×3 となって PB(x)の長さを測れば 積(2.5×3)が解る。 |
|
| 解答:直径を「円周率分の1で刻まれた目盛」(丸目という)を使って測ればよい。丸目で測った値は直径の円周率倍(直径×円周率)となっているので,その値が円周の長さになる。 |
解答; 2.5×3 を例に説明します。(三角形の相似を利用)
|
 |
| 理由: PQとACが平行だから △PBQと△ABCは相似となり,対応する線分の比が等しいので PB:AB=QB:CB よって x:2.5=3:1 だから 外項の積と内項の積が等しいから x=2.5×3 となって PB(x)の長さを測れば 積(2.5×3)が解る。 |
|
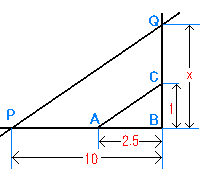
| 解答:(割り算は掛け算の逆) 例えば,10÷2.5 を考える
|
 |
| 解答: 正方形ABCDの一辺の長さを10cmとするとき,AD上の正八角形の頂点K,Lを見つけるには AL,DKの長さを,実際のルート2倍の目盛(曲尺の角目)で,5(実際は5のルート2倍の長さ)の点を,それぞれL,Kとする。 他の辺においても同様にE,F,G,H,I,J,を見つける。 この8点が正八角形の頂点となる。 |
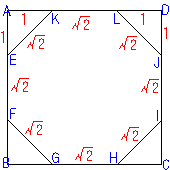 |
理由: すなわち,ALやKDは5cm(正方形の1辺の半分)のルート2倍の長さとなるので, 正方形の一辺の半分の長さを角目で測ることによって,正八角形の各頂点を求めることができる。 |
|
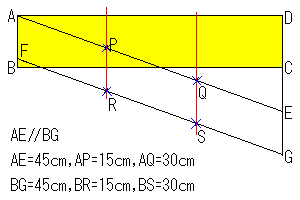
解答:
|
 |
||||||||
| 理由: 三角形の相似や平行線と線分の比を使って説明できる。R,Sは求めなくてもP,Qだけでも可能だが,ABと平行な直線がより簡単に引ける。 |
|||||||||
| これを応用すれば,曲尺の裏目(表目の1.41421356・・・倍)の目盛だって簡単に引くける。 | |||||||||
曲尺は計算尺にもなったんです。今日ならまさに電卓ですね。デジタルの電卓より,アナログの曲尺のほうが,材木等を直接測る事ができて,作業もスムーズに運び,実用的だったかとも思います。大工さんたちの知恵には感心するばかりです。