暇つぶしに
数学（？）に挑戦しよう！

「三平方の定理」の証明と「ピタゴラス」
「証明方法，沢山あるんですって？」と，質問を受けて

　
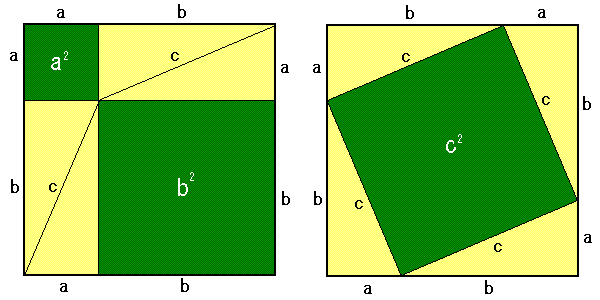
三平方の定理の証明　その１
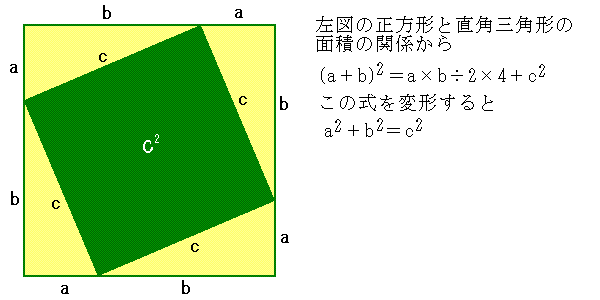
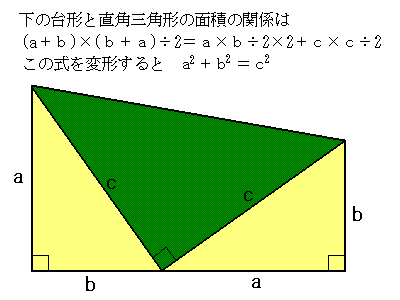
　上の図は，左右とも，１辺がａ＋ｂの正方形の中に３辺がａ，ｂ，ｃの合同な直角三角形（黄色）が４個あり，残りは正方形（緑色）です。そこで ａ2＋ｂ2＋ａ×ｂ÷２×４＝ｃ2＋ａ×ｂ÷２×４ よって ａ2＋ｂ2＝ｃ2 が成り立ちます。三平方の定理の証明って意外と簡単ですね。
　
三平方の定理の証明　その２
 
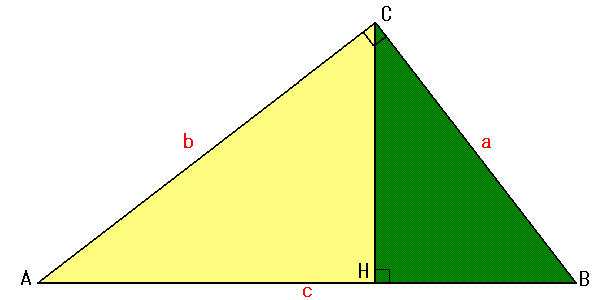
三平方の定理の証明　その３
△ＡＢＣと△ＡＣＨが相似だから　ｂ：ＡＨ＝ｃ：ｂ　即ち　ＡＨ＝ｂ2÷ｃ
△ＡＢＣと△ＣＢＨも相似だから　ａ：BＨ＝ｃ：ａ　即ち　ＢＨ＝ａ2÷ｃ
だから　ｃ＝ＡＨ＋ＢＨ＝ｂ2÷ｃ＋ａ2÷ｃ　よって　ａ2＋ｂ2＝ｃ2
　
三平方の定理の証明　その４
 
三平方の定理の証明　その５ 三平方の定理の証明方法は１００通り以上あるようです。私自身そんなには知りませんが，わかり易いというか，簡単そうなものを幾つか紹介してみました。他にもいろいろ，考えてみるのも面白いかと思います！
　
　
　誰でも知っている最も有名な数学の定理かも知れません。ピタゴラスの定理（「ピタゴラスの定理」と呼ばれていたのだが，戦時中の敵国言語禁止で考案されたのが「三平方の定理」というが，実に的を射た名前かと）ともいいますが，ピタゴラス（Pythagoras　ＢＣ560？～480？）自身が発見したのではないという説も。ピタゴラスはエジプト（土木・測量技術や天文学の先進地）を旅した後，南イタリアのクロトーネに学校を開きますが，その学校で知ったり発見したことは部外秘，弟子たちが発見したものも全てピタゴラスの業績として伝えられているとも。この定理も，エジプトで測量術として利用されていたもので，ピタゴラス（学派）が論理的に説明（証明）したものです。しかし，発見がピタゴラスでなかったとしても，彼の評価が変わることはないでしょう。彼らの論理的な証明や発見が，エジプトの「実学」を自然科学の女王「数学」として大きく開花・発展させた訳ですから。
　a2 ＋b2 ＝c2 を満たす自然数 a，b，c のことをピタゴラス数と言います。３，４，５ や ５，１２，１３ などです。この３つの数を３辺とする三角形は直角三角形で，古代エジプトでは縄張り師という人々が正確な直角を作るのに利用しました。ピラミッド建設にも利用したのでしょう。ところで，３，４，５のような連続したピタゴラス数は，他にもあるのでしょうか。連続した３つの数を ｘ，ｘ＋1，ｘ＋2 とすると，ｘ2＋（ｘ＋1）2＝（ｘ＋2）2 この方程式を解くと ｘ＝3，-1　ここで ｘ＞０だから ｘ＝３ よって 連続するピタゴラス数は ３，４，５ だけです。
　
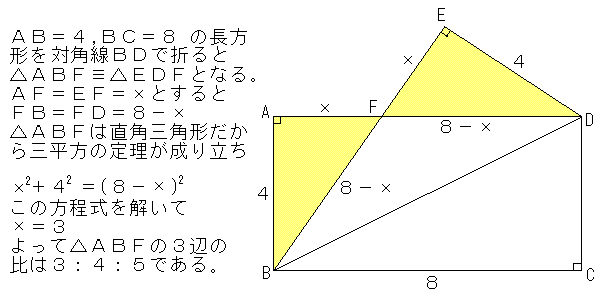
　この３，４，５を３辺とする直角三角形が身の周りにあるなんて考えもしませんでしたが，
ピタゴラス数の三角形
　以上のように，３：４：５の比を持つ直角三角形は，たてと横の辺の比が１：２の長方形から簡単に見つける事ができます。正方形の折り紙を半分に折れば，辺の比が１：２の長方形です。よって，折り紙を２回折るだけで見つかります。最も簡単なピタゴラス数の三角形，意外と身近なところにあるんですね。他にも，辺の比が１：３の長方形からも可能です。これも簡単に証明できますので，挑戦してみましょう！（参考図書：Yoshita著，星の環会発行の「美しい数学2」　美しい絵がいっぱいで，数学の世界が楽しく覗けます，まさに絵本のような本でした）
　
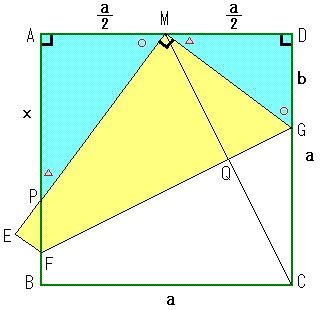折り紙を三等分に　ところで，折り紙を三等分に折ることができますか。二等分や四等分だったら簡単ですが，三等分は難しそうですね。しかし，意外と簡単に見つかります・・・

　右図のように，正方形ABCDの頂点Cが辺ABの中点Mと重なるようにFGで折り曲げ，辺BC（EM）と辺ABの交点Pを求めると，PBはちょうどABの３分の１です。

＜証明＞
　正方形ＡＢＣＤの１辺の長さを ａ，DG＝ｂ とすると CG=MG=ａーｂ だから
　直角三角形ＭＧＤで 三平方の定理が成り立つ（MD2＋DG2＝MG2）ので
　（ａ/２）2＋ｂ2＝（ａーｂ）2
　よって ｂ＝（3a）/8
　また △APM∽△DMG だから AP＝ｘ とすると
　AP：DM＝AM：DG だから ｘ：a/2＝a/2：（3a）/8
　よって ｘ＝（2a）/3
　すなわち 点PはABの三等分点です。
　正方形を２回折るだけ，意外と簡単に三等分点を見つけることができます。

　これも三平方の定理を使って証明できました。
　
　ピタゴラスは「数は万物の根源である」と主張しているだけあって，いろんな数を考えています。三角数（６＝１＋２＋３　などの１から始まる自然数の和で，正三角形の形で表すことができる数）や，四角数（９＝１＋３＋５　などの１から始まる奇数の和で，正四角形で表すことができる数）とか，完全数（６＝１＋２＋３ というように，その数「６」を除く約数１，２，３の和に等しい数）などです。三角形の内角の和が２直角であることや正五角形の作図法，無理数の発見などもピタゴラス（学派）の業績です。
　

　定理とは「公理に基づき，論証によって証明された命題」，簡単に言えば「誰でもが正しいと納得する筋道で説明できた文」で，証明とは「誰でもが正しいと納得する筋の通った説明」となるのでしょうか。
　この証明の技法を確立したのがタレス（Thales　ターレス　ＢＣ624？～ＢＣ546？）で，彼が証明したものに「対頂角が等しい」「三角形の合同条件」「直径に対する円周角は直角」などの定理が。このタレスの教えがピタゴラスをはじめとするギリシャ数学に大きな影響を与えます。ピタゴラスにエジプト行きを勧めたのもタレスとのこと。
作成：2008/01/24　最終更新：2009/02/23

メニューにもどる