彦一どんと殿さん
 とんちで有名な彦一が，八代の殿さんから手柄のほうびをもらうことになります。
「彦一，何でちゃよか，おまえの好きなものをほうびに与えるから，好きなものを申せ。」
「いや，たいしたこつぁしとらんけん，いりまっせんバイ。」
「何ば言うとるか。やると言うんだから，何でんよかから，申せ。」
「殿さん，本当に何でん良かとですか？」
「俺は殿さんバイ，何でんでくるけん，申せ！」
そこで，彦一の言うことには，
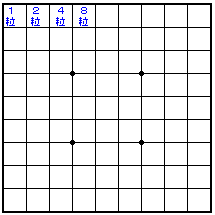
「殿さんな，将棋ば好（し）ートンナハルですね。将棋盤の最初の”ます目”に米を１粒置いてくだはり。２番目の”ます目”には２粒，３番目には４粒，４番目には８粒，・・・・・というふうに，将棋盤の最後の”ます”まで米粒を置いていって，将棋盤全体に置く米粒バもらおっごたっとバッテン，良かですか？」
「何や，そんくらいか。彦一は欲んなかな。よかバイ。持ってけ，持ってけ。」
「本なこつ，良かっですか？ そんなら証文ば書いてくだはりまっせ。」
殿さんな「将棋盤の各ますに，次々と倍々にして置いていく米粒を彦一に与える」という約束を，文書にして渡しました。
ところで，この米粒の量は，どれだけになるのでしょう？
殿さんは彦一との約束を果たすことができたのでしょうか？
この米粒の数を計算してみましょう。
１＋２＋４＋８＋１６＋３２＋６４＋１２８＋・・・・
将棋盤のますの目は，８１（＝９×９） ですから，
初項が１，公比が２の等比数列の，初項から第８１項までの和となります。
よって等比数列の和の公式を使えば，「２の８１乗－１」 となります。
これは，２５桁の数となります。２５桁の数で最も小さい数でも，
１００００００００００００００００００００００００（＝１０の２４乗）
米粒１００粒で１ｇとすれば，１０００００粒で１ｋｇ，１００００００００粒で１トン。
１００００００００００００粒で１万トンとなります。すなわち，１０の１２乗粒で１万トンです。
日本で年間生産量は約１０００万トンだから，１０の１５乗粒です。
よって，彦一がもらおうとした米粒の量は
（１０の２４）乗÷（１０の１５乗）＝１０の９乗＝１０００００００００
すなわち，日本全国で生産される米の「１０億年」分です。
八代の殿さんが自由にできる米の量ではありません。
またしても，彦一のとんちにやられた殿さんでした。
|
実際に計算すると，米粒の数は2417851639229258349412351（写真部の茶谷さんがそろばんを使って計算してくれました）
米５０粒で１ｇ（理科実験室で白米を計ってみました）となりますので， 日本全国の生産量の約５０億年分になります。
２の８１乗という数というのは，とつけみにゃあ太か数です。
|
|