「指算」についてまとめた
普通科3年の土山君のレポ-トを紹介します。
![]()
乗法の九九の中の「1×1」から「5×5」までを覚えていれば,「15×15」までを,「指」で計算することが出来る方法を紹介します。
| 【例1】 | 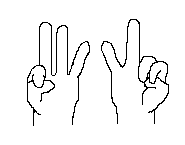 |
7×8の計算の場合 |
| 立っている指 3×2=6 → 1の位 折りまげた指 2+3=5 → 10の位 これから 50+6=56 |
||
| 【例2】 |  |
6×6の計算の場合 |
| 立っている指 4×4=16 → 1の位 折りまげた指 1+1=2 → 10の位 これから 20+16=36 |
||
| 【例3】 | 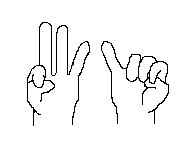 |
12×14の計算の場合 |
| 折りまげた指 2×4=8 → 1の位 折りまげた指 2+4=6 → 10の位 これから 100+60+8=168 (この100という数は10×10から) |
というふうに,指を使って計算することが出来る。一般化すれば,次のようになる。
| 【例1】 と 【例2】 |
(1けたの数×1けたの数)の場合 |
| ①立っている指どうしかける → 1の位 ②折り曲げた指どうしをたす → 10の位 ②+①と計算する。 |
|
| 【例3】 |
(2けたの数×2けたの数)の場合 |
| ①折りまげた指どうしをかける → 1の位 ②折りまげた指どうしをたす → 10の位 ③(10×10=100) ③+②+①と計算する。 |
それでは,証明してみよう。
| 【例1】 と 【例2】 の 証明 |
|
||||||||||||
| 立っている指 (10-χ)×(10-y) → 1の位 | |||||||||||||
| 折りまげた指 (χ-5)+(y-5) → 10の位 | |||||||||||||
| として,計算結果を出せば (10-χ)×(10-y)+10{(χ-5)+(y-5)} =100-10y-10χ+χy+10χ-50+10y-50 =χy すなわち,(1けたの数×1けたの数)が計算出来ることになる |
| 【例3】 の 証明 |
|
||||||||||||
| 折りまげた指 (χ-10)×(y-10) →1の位 | |||||||||||||
| 折りまげた指 (χ-10)+(y-10) →10の位 | |||||||||||||
| として,100を足せば(100の位に1) (χ-10)×(y-10)+10{(χ-10)+(y-10)}+100 =χy-10χ-10y+100+10χ-100+10y-100+100 =χy と証明することができる。 |
| 感想: | 日本では,九九を小学校のころに覚え,1×1から9×9までの計算をみんなが知っている。しかし,外国では日本のような九九が無く,九九を暗記していないので,このような指算を使って計算しているという。簡単な九九を知ってる日本ではこんな計算法は使われることはないと思うが,このような方法で掛け算ができるということを知り,数学への興味と関心が増したようにも思える。様々な工夫や発見に驚きます。しかし,九九というものは何とすばらしいものでしょう。 |
作成:パソコン同好会(2001/04/13)