|
問題1
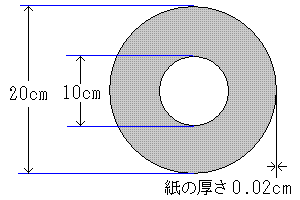 右図のような直径10cmの芯に直径20cmの大きさまで巻いたトイレットペーパーがある。トイレットペーパー1枚の厚さを 0.02cmとして,このトイレットペーパーの長さを求めよ。 右図のような直径10cmの芯に直径20cmの大きさまで巻いたトイレットペーパーがある。トイレットペーパー1枚の厚さを 0.02cmとして,このトイレットペーパーの長さを求めよ。
ヒント:解き方もいろいろ。半径rの円の面積は πr2 ,円周の長さは 2πr である。トイレットペーパーを真横から見た図形の面積を「巻いた形(右図)」と「引き出した形(長方形)」で求めて,それらが等しいという関係や,一番外側は直径20cmの円,外から2番目は直径20-0.04cm,その次は20-0.04×2,・・・,そして一番内側の
10+0.04cmまでの同心円の円周の合計(等差数列の和)をトイレットペーパーの長さの近似値と考えてもいいかな。(解答例:円周率を3.14として計算すると,面積からは
117.75m ,数列の和からは 117.907mに) |
|
| 問題2 |
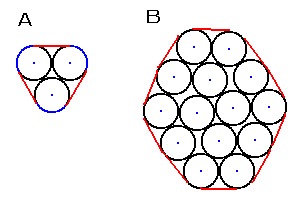 右図のように,半径10cmのトイレットペーパーをひもでしばりました。AとBの場合について,ひもの長さはそれぞれ何cmとなるか。 右図のように,半径10cmのトイレットペーパーをひもでしばりました。AとBの場合について,ひもの長さはそれぞれ何cmとなるか。
ヒント:Aは円弧の部分(青の部分)は各円周の3分の1だから簡単かな。それに比べてBは複雑そう。しかし,円の接線は,その接点を通る半径に垂直,図をうまく使えば,両方とも同じような考え方で求められることに気付くのでは。円弧の部分と線分の部分に分けて考える。線分の部分は直径に等しい。円弧の部分は弧の中心角を求めなければならない。部分部分で計算しようとすると,ややっこしそうだが,全体を見渡せば,簡単な方法が見つかりそう。右図にマウスオンでヒントが。ところで,この問題はトイレットペーパーでなく,空き缶のほうが歪みが少なく,問題としては的確だったかとも。(A:20π+60cm,B:20π+200cm) |
|
| 問題3 |
本校で使っているトイレットペーパーを測ってみると,芯の直径が約4cm,全体の直径は約10cmで,長さは55mと表示されています。このトイレットペーパーは,使い切るまでには約何回転するか計算せよ。
ヒント:問題1がヒント。トイレットペーパの厚さから,回転数(巻き数,同心円?の数)が解る。(約250回転) |
|
|
| 掃除担当区域が西階段。その1階にトイレットペーパーの保管所があります。トイレットペーパーを両手いっぱい抱えていく姿が本ページ作成の糸口。巻紙は図形的にも面白いというか興味深い形です。トイレットペーパーに関する問題は他にももっとできそうです。問題作りにも挑戦しましょう。問題って解くだけでなく,自分で創作するのも面白いかと思います。(2006/10/28) |