暇つぶしに
数学（？）に挑戦しよう！

πについてまとめた
普通科３年の安倍君のレポートです。

πについて

　円周率πは，円の周や面積の計算にどんどん使われるとても役に立つ数です。それなのに，そのπの値をちゃんと書き表そうとすると，

　３．１４１５９２　６５３５８　９７９３２　３８４６２　６4３３８　３２７９５　０２８８４　１９７１６　９３９９３・・・・・

　となって，「・・・・」の後は，いくつでも続いて終わりがありません。それに，

　０.１４２８５７　１４２８５７　１４２８５７　１４２８５７　１４・・・・

のように「くり返し」（循環小数）にもならないのです。

　このような不思議な数を使いこなすために，ある人たちは，自由に大胆な実験や計算をしました。このレポートはそのπの値を簡単に求める実験や計算についてまとめてみました。

～古代の道具でπを測る場合～

　昔は，私たちが今持っているような便利なコンパスや正確な定規もありませんでした。仮に１本の糸と木切れしかなかったとして，どれくらい正確に測れるかという実験。　
　まず，糸の両面に木切れをくくりつけて地面に円を描き，そしてその糸をそのまま定規の代わりにして円周を測っていきます。糸を円に重ねて糸の長さ（半径）ごとに目印をつけていきます。

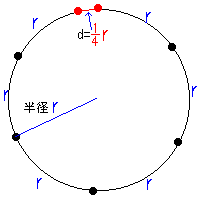　目印は６回付けられて少し余ります。そこで糸を四つ折りにしてその余りにあててみると，かなりよく合います。円周を ｌ(エル)，半径を r，余りの長さを ｄ とすると		 半径ｒの円
　今説明したことから

　ｌ（エル）＝６ｒ＋ｄ
　ｄは，半径の１/４　に近いので，ｄ≒ｒ/４　と表せます。

　従って，　ｌ ≒ ６ｒ＋1/４ｒ＝２（３+１/８）ｒ　となって

　円周を求める式は，ｌ＝２πｒ　だから　π≒３＋１/８＝3.125　となる。

　木切れと糸だけでも，これだけ正確に測ることが出来ました。ちなみにこの円周率の求め方は，バビロニア（メソポタミアの古代都市）で使われていたものです。
～自転車の車輪で円周率を測る場合～

　自転車の車輪の半径と進んだ距離で，円周率を測る実験もあります。まず，自転車の車輪の半径を測ります。車輪の半径は，３３．１ｃｍでした。
　次に，この自転車の車輪を１ヵ所に目印を付け，１周したら分かるようにしておきます。車輪がちょうど８回転するまで直線上を押していきます。そして８回転したところで，その距離を測ります。

　８回転して進んだ距離は，次のようになりました。
　（１回目）１６．４０ｍ　　（２回目）１６．４４ｍ

　これらの平均の１６．４２ｍを車輪一回転分に進んだ距離（車輪の円周）ｌを求めるため８で割り，円周を求めます。　ｌ ＝２０５ｃｍ

　πは，円周÷直径　で求めることができるので
　π≒円周÷直径＝２０５／（２×３３.１）＝３.１０６・・・・　となる。

　そして求まった数の小数第３位を四捨五入し　3.11
　この数も円周率(3.14)にかなり近い数を求めることができた。

　（８回転より，10回転のほうが計算しやすかったかな，反省！）
～五円玉で円周率を測る～

　自転車はおおがかりで大変なので，五円玉を使って円周率を自分で測ってみた。やり方は，五円玉を自転車の車輪にみたて，さきほどと同じように五円玉の直径を測り，５回転させその距離を回転数で割り直径で割るというものです。
五円玉の直径は，２．１ｃｍでした。

５回転して進んだ距離は，次のようになりました。　
（１回目）31.5　（２回目）33.5　
この結果の平均を求め回転数で割り，それを直径で割ります。
　π＝3.0952381
　四捨五入して　3.10　

（この測定はあわてたためか，五円玉が滑って少々誤差が大きかったようだ，反省！）

～感想～

　以上の実験からは，せいぜい小数点以下１桁ぐらいしか正しい値を出すことが出来ませんでした。それでも，これだけの単純で簡単な実験だけである程度正確な値を出すことが出来ました。学校では，「πが3.14だよ！」としか教わらず，「どうやって円周率を求めたのか」が気になっていました。今までは，πの値を求めるのは大変難しいことで，自分には出来ないとばかり思っていたけれど実際に調べ，ここまで分かるとは正直思っていなかった。このπの事を調べてまだ知らないところや分からないところはあるけれど，ほんの少しだが数学を考える楽しさが分かったように思える。ちなみに，円周率の近似値値３．１４から３月１４日が円周率の日，数学の日とのことです。

作成：パソコン同好会（2001/04/13）

メニューにもどる