- 問題1.
- 図1と図2の円は全く同じ大きさです。それぞれの方法で円の面積を求めなさい。
完全に円の中にあるマスは[ ]個
一部が円にかかるマスは( )個で,完全なマスの半分と考えます。
| よって 面積 = |
[ ]×1+( )×0.5 |
| = |
(cm2) |
|
図1
1マスは 1cm×1cm=1cm2 |
 |
完全に円の中にあるマスは[ ]個
一部が円にかかるマスは( )個
| よって 面積 = |
[ ]×0.25+( )×0.125 |
| = |
(cm2) |
|
図2
1マスは 0.5cm×0.5cm=0.25cm2 |
 |
| この考え方で1マスの大きさを小さくしていけば,より正確な円の面積を求めることができます。円の面積=円周率×半径2 よって円周率=円の面積÷半径2 。だから,より正確な円周率を求めることも。円全体では数えるのが大変だったら,4分の1円を数えても良いでしょう。1マスの大きさを次々と小さくするのは限界があるなら,半径を大きくしていっても良いのでは。どちらにしても限界はありますね。 |
|
|
- 問題2.
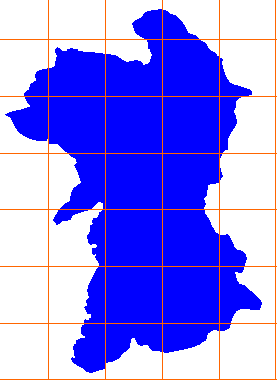
- 右図は島の部分を除いた熊本県の地図です。面積を求めなさい。単純化するため島を除きました。地図の縮尺(マスの大きさ)は大まかなものであることをお断りしておきます。
完全に熊本県の中にあるマスは[ ]個
一部が熊本県にかかるマスは( )個
| よって 面積 = |
[ ]×400+( )×200 |
| = |
(km2) |
参考までに,1マス10km×10kmの図も |
1マスは 20km×20km=400km2 |
 |
一部が図にかかるマスの面積の平均を,完全なマスの面積の半分とみなしましたが,目測でそれぞれ 02とか 0.6などと細かく計算すれば,精度が高くなります。
様々な縮尺の地図上の面積も求めることができます。5mm方眼紙を使って2万5千分1地形図上の面積を求める場合,5mm(5mm×25000=125000mm=125m)は実際には125mだから,5mm方眼紙の1マスは15625m2(125m×125m) として計算すればいいでしょう。おおざっぱでいいのなら,適当な大きさのマス目を自分で引いてもいいでしょう。
幼稚な方法に見えるかも知れませんが,このような考え方を発展させたのが区分求積法で,微分・積分にもつながっていきます。 |
|


