負の数について調べた
普通科３年の前田さんのレポートを紹介します。

●負の数とは●

　文明が高くなると，どんどんと「大きな数」や「小さな数」が必要となります｡昔は，１より小さい数は，すべて「分数」で表されていたのですが，１５８５年に『シモン・ステビン』が現在の「小数」という考えを提案しました｡小数によって，０より大きい「微小な数」を繊細に表現できるようになりました｡
☆「５から３は引くことが出来ても，３から５は引くことが出来ない」で処理されていたのです｡当然，３から１０を引くこともできません｡どちらも出来ないのですが，「出来なさ」の程度が違うのです。

例	３冊の本があるとします｡５人の人がやって来て，次は１０人の人がやって来ました。１人に１冊ずつ配るとしたら，どちらも不足します｡しかし，不足の程度が違うのです｡５人来たときは２冊足りないし，１０人来たときは7冊足りません。

　この「不足」を表現するために「－」という印をつけて表すと，
　　３－５＝－２
　　３－１０＝－７　と書けます｡

　長い時間が必要でしたが，これは便利だということで，次第にこのような数が一般的に認められるようになってきました｡そして，『負の数』と呼ばれるようになりました｡

　３人来た場合は，本は１冊も残りません｡このことを「0」という数字で表して，
　　３－３＝０　と書けます。

　この「０」を基準にすると，負の数はそれより小さい数となります。今までごく普通に使ってきた数は０より大きい数となります。そして，負の数に対抗して，『正の数』と呼びます｡

●負の数の入った「たし算」と「ひき算」●

　「十」，「一」は数直線上で，０より右，左という意味以外に，たし算，ひき算という意味があります｡□＋３とは□をスタート点として，右へ３単位進む，□－３は□をスタート点として左へ３単位進むという意味です｡
　右へ進む，左へ進むという動きがたし算，ひき算ということになります｡

●３より５大きい数は？●

　式で書くと「３＋５」となり，もっと詳しく書くと，「0＋3＋5」となり，数直線上では，基準となる「０」からスタートして，右へ３単位，さらに右へ５単位進みます｡

●３より５小さい数は？●

　式で書くと｢３－５｣となり，詳しく書くと｢０＋３－５｣となり，数直線上では，０から右へ３単位，さらにその場所から左へ５単位進みます｡といういことで「－２」になります。

●３よりー５大きい数は？●

　－５大きいという言い方は不自然です｡「＋」，「－」にはちょうど正反対のことを表します｡「－５大きい」とは「５大きい」の反対という意味なので｢５小さい｣ということなのです｡すると，
３より－５大きい=３より５小さい
となり，｢３－５｣のことなのです｡３より□大きいとは，３＋□のことなので，３より－５大きいをそのまま式に表すと，
「３＋（－５）」となります｡つまり，
「３＋（－５）＝３－５」ということなのです｡

●３より－５小さい数は？●

　式にすると，「３－（－５）」となります｡「－５小さい｣を普通の言い方にすると，｢３より５大きい数は｣となるので，「３＋５」のことなのです。つまり，
「３－（－５）＝３＋５」ということなのです。

※＋（＋），－（＋）の部分は，いつも「＋」，「－」になります｡これは次の２つの約束をしておくのと同じです｡

このように約束しておくと，次の（イ），（ロ），（ハ），（ニ）は

（イ）	●＋（＋３）	→	●より（＋３）大きい
（ロ）	●＋（－３）	→	●より（－３）大きい
（ハ）	●－（＋３）	→	●より（＋３）小さい
（ニ）	●－（－３）	→	●より（－３）小さい

となります。

ここで，次の約束をします｡

すると，先ほどの（イ），（ロ），（ハ），（ニ）は

（イ）	●＋（＋３）	→	●より３大きい
（ロ）	●＋（－３）	→	●より３小さい
（ハ）	●－（＋３）	→	●より３小さい
（ニ）	●－（－３）	→	●より３大きい

となります。

☆（＋３）－（＋５）だと最初の（＋３）は０より（＋３）大きい。つまり，３大きいことで，後ろの－（＋５）は＋３より（＋５）小さい。つまり，（＋３）より５小さいことです｡　これを簡単に書くと，｢３－５｣のことで，数直線上で説明すると，

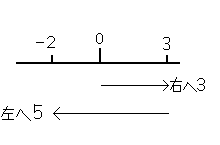　０から出発して｢右へ３｣，さらにその場所から｢左へ５｣進んだところなのです｡

　今までのところをまとめてみると，

規則	＋（＋●）→＋● ＋（－●）→－● －（＋●）→－● －（－●）→＋●

◎同符号の場合は｢＋｣，異符号の場合は「－」となるのです。

作成：パソコン同好会（2001/04/13）

メニューにもどる